Butterfly valve disc deflection estimation method
1.preface
simple butterfly valve structure, small size, light weight, and has a certain degree of flow control features.
The butterfly valve heart parts- disc plays the role of cutting off medium when the valve is closed, and affected by media pressure differential of both ends before and after the valve to occur deformation, the deformation size of the valve has a greater impact to sealing performance, sealing surface itself wear and switching operating torque. Therefore, the more accurate estimates and research of disc deflection, it is reasonable to choose and design the structure size of the valve, and takes this as the basis for selection, designing transmission mechanism and adjusting the implementing devices.
2.stress analysis
Butterfly valve spindle inserts into disc, by four long tapered fastening pin, can take spindle and disc as a whole. Between the spindle and sleeve is the gap matching, in the calculation of deformation, it can approximately take the disc seemed as the simply supported bearing type variable cross-section beams. The disc is circular, the load that along disc axial direction is uneven, as shown in Figure 1
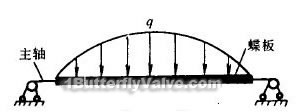
disc that is affected by the media force, the beam will occur bending, if the stress within the elastic limit, the whole deformation within the beam as follows:
formula (1) only considers the bending moment effects. In addition, each module will also store a certain degree of shear strain energy, which is much smaller than the bending strain energy, is negligible. From Castile Lane Arnold (Gastigliano) first theorem to get:
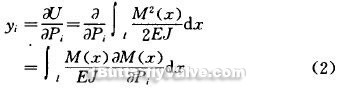
formula (2) shows that: if a number of external forces (generalized force, including the moment) affect on one elastomer, then the elastomer deformation energy U for any external force Pi partial derivatives is equal to the force of the acting point along the the direction of force deformation yi, as shown in Figure 2
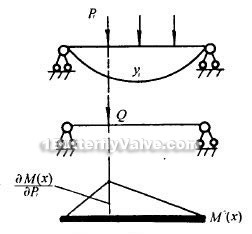
concerning the disc, quadrature and partial derivatives are very difficult. According to Maxwell (JG Marwell) - Moore (O. Moho) principle that,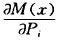
in formula (2) can be seen as the same beam Pi acting point, bearing the effect of one unit load along Pi direction that causes bending moment M ° (x), that is,
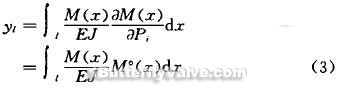
formula (3) points is still very difficult, because M0 (x) change is relatively simple, M (x) is a a function that changes by x, disc is circular, and its thickness along the axis X also is not a fixed value, Therefore, the disc inertia J is actually varies with the X and more complex function J (x).
formula (3) can use weilih Saint-Venat proposed simple algorithm. This algorithm is simple and described as follows: makes EJ = cont (fixed value)
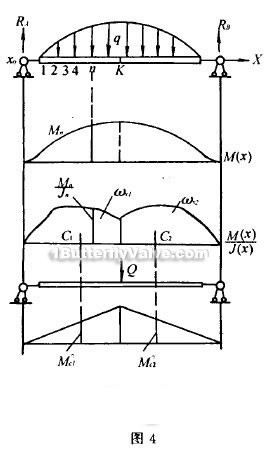
If you require any point K displacement, it can act a unit virtual afterburner Q on the K point, and make M (x), M ° (x) diagram, shown in Figure 3.
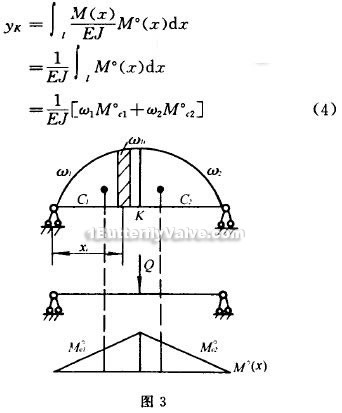
formula (4) shows that: knowing deflexion only need to calculate M (x) picture area (ω1, ω2), and multiplied the vertical coordinates M ° l that just below centroid area M ° (x) diagram. If M (x) is complex, and very difficult to calculate them, the area of ω1, ω2 and focus of cl, c2 can be applied to mapping derived. Using area of ω1, ω2 sub-taking moment method derived cl, c2, the section is more detailed, and with more accurate results, each center of gravity can be approximated to take snippets of each subparagraph ωi center. Then
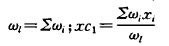
The disc studied here, J (x) is also a very complex function and, therefore, can use weilih Saint-Venat method to calculate, namely, the picture multiplication evaluatation.
As mentioned above, find disc deformation, can divide the disc along the axis X direction into many sections 1,2,3 ... n, n +1 ..., and find the X-axis perpendicular to the direction of sections in the paragraphs J,, JZ, J3 ... Jn, Jn +1 ".. value is used, and then find the various sections of M1, M2, ... Mn, Mn +1 ... values, shown in Figure 4
According to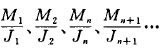
…series data, we make the picture of
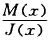according to the proportion, That is to indicate the M (x), J (x) complex function relationship with a graphics.
3、Deflection Analysis and Calculation
If required beam deflection YK of any point, in the K-point increase the imaginary unit force Q, and to make the M 0 (x). This allows the use of weilih Saint-Venat diagrammatic multiplication method to calculate. In this case, formula (4) has the following form:
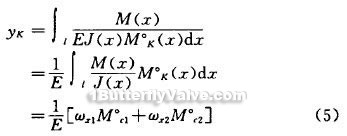
formula ωx1, ωx2-M (x) / J (x) Graphic Area
As we nearly take the disc to be considered as a simple beam, therefore, using formula (5) to calculate or derived by multiplying the deflection y values are disc in the Z direction of each vertical section that all points have the common deflection, vertical section KK's deflection yK-K are equal, Figure 4. However, Z-axis direction deflection in fact not equal, such as the edge K-point deflection should be larger than deflection y0 of center 0, that is, there should be another deflection, this deflection is uner the effect of force q, by the Z-axis direction bending moment generated.
Taking A-A axis as a fixed end, taking Z-axis direction half disc D / 2 as a cantilever beam, its deflection can be approximately considered to be Z-axis direction parallel to the X-axis deflection of each section.
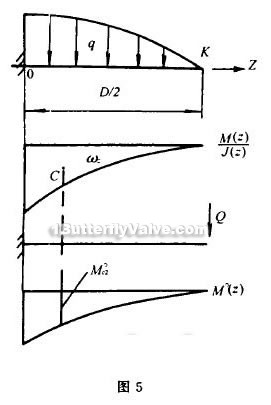
Z-axis direction deflection y: Similarly, according to the multiplication of weilih Saint-Venat. To calculate the disc edge K point maximum deflection yKZ is also the same that add a virtual unit force Q on the K point (see Figure 5), then are:
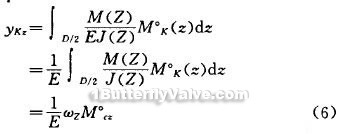
in the formula, ω2 --- m (z) / J (z) Graphic Area
According to the superposition principle, the deflection y of any point of the disc should besum of the X-axis direction simple beam deflection y2 and Z-axis cantilever beam deflection y2, namely:
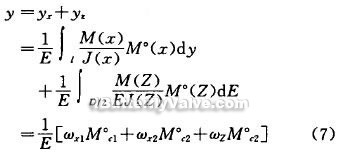
formula (7) is to use diagram multiplication to calculate the disc deflection formula
4.Conclusion
Taking the disc approximately as the beam conditions to calculate the deformation, in the calculation of one position deformation, ignoring the impact of another direction, but this effect would bound the deformation of disc. Using this method, to calculate the deflection is relatively similar, the calculated result is too large, but it is safe and allowed for the engineering design.
